
Números Imaginários
Ao longo da história muitas civilizações chegaram na solução da equação quadrada (de segundo grau), ax2 + bx + c = 0, que é a famosa fórmula de Bhaskara que aprendemos na escola [1]. Porém, algumas formas específicas dessas equações aparentavam não ter solução. Tomemos como exemplo x2 + 1 = 0. O resultado seria √(-1), o que não faz sentido, já que não existe raiz quadrada de números negativos (pelo menos no mundo real) [2]. Em 1494, o frade italiano Luca Pacioli publicou um livro intitulado “Summa de Arithmetica”, no qual englobava todo o conhecimento da época a respeito de álgebra e geometria. Um dos problemas em aberto era o da equação cúbica (de terceiro grau): ax3 + bx2 + cx + d = 0. Pacioli afirmou em sua obra que não existia solução para essa equação [1,3]. Parte disso se deve ao fato de que, desde a Antiguidade até meados da Idade Moderna, os matemáticos não pensavam nos problemas somente por fórmulas como fazemos hoje, mas sim em palavras, poemas e formas geométricas. Uma maneira de provar a fórmula de Bhaskara, por exemplo, é usando a área de quadrados e retângulos (veja aqui). Porém, isso é mais complicado no caso da equação cúbica [1]. No início do século XVI vários matemáticos estudaram o problema da equação de terceiro grau, dentre eles estão Scipione del Ferro, Niccolò Fontana Tartaglia, Girolamo Cardano e Rafael Bombelli [1,3]. Del Ferro obteve a solução para a equação cúbica reduzida (sem o termo x2, ax3 + bx + c = 0) de forma geométrica utilizando cubos, mas não revelou sua descoberta a ninguém. Na época, ter a solução de um problema era como ter uma arma estratégica, pois era comum haver “duelos” entre matemáticos em que cada um dava uma seleção de problemas para o outro resolver [1]. Tartaglia também encontrou a solução para a equação cúbica reduzida, e acabou compartilhando-a com Cardano depois de muita insistência. Cardano, porém, empenhou-se em tentar solucionar a equação cúbica completa, incluído o termo x2. Ele de fato conseguiu esse feito através de substituições que faziam o problema ser simplificado ao caso da equação cúbica reduzida [1,3]. No processo de solução dessas equações ainda apareciam as raízes de números negativos, o que Cardano interpretou como uma espécie de “área negativa”. Mas agora, ao contrário do caso da equação do segundo grau onde a solução não existia, essas raízes de números negativos eram usadas como passo intermediário para chegar na solução correta, resultando em um número real [1]. Rafael Bombelli mostrou posteriormente que os termos que continham raízes de números negativos nas fórmulas de Cardano podiam ser reduzidas a a + b√(-1), sendo chamados de números complexos. E Leonhard Euler popularizou a notação de i = √(-1) como sendo a unidade imaginária [1]. O fato da representação matemática, de algo que existe apenas de forma abstrata, poder resolver problemas reais é realmente surpreendente. Um dos exemplos mais interessantes disso está presente na Física através da equação de Schrödinger: Quando Schrödinger adicionou nela a unidade imaginária i, ele conseguiu obter as soluções da função de onda Ψ(r, t) que correspondem às órbitas quantizadas do átomo de Bohr! Isso mostra que a natureza funciona com números imaginários. E a descoberta de i tornou-se uma ferramenta fundamental para ajudar-nos a entender a realidade [1]. Texto por: Cristhian Gean Batista Guimarães. Referências: [1] Veritasium. How Imaginary Numbers Were Invented. YouTube: 1 nov. 2021. Disponível em: https://youtu.be/cUzklzVXJwo?si=NtIb8OK3KDwOzoHJ. Acesso em: 18 set. 2023. [2] Welch Labs. Números Imaginários são reais [Parte 1: Introdução]. YouTube: 28 ago. 2015. Disponível em: https://youtu.be/T647CGsuOVU?si=0Fxd1cy_IZzTNGGF. Acesso em: 18 set. 2023. [3] NAHIN, P. J. An Imaginary Tale. New Jersey: Princeton University Press, 1998.
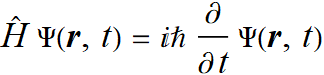
Cara que incrível mds
Texto muito interessante e fico feliz de tê-lo encontrado estudando os números imaginários, põe bastante em perspectiva como foi chegado no conhecimento e os percalços históricos, algo pouco citado quando se estuda matemática