Efeito Dzhanibekov – Teorema da Raquete de Tênis
Em 1985, o cosmonauta Vladimir Dzhanibekov estava na estação espacial soviética Salyut 7. Essa ocasião rendeu fatos memoráveis, já que a estação teve um problema elétrico e todo o seu controle foi perdido. Com o esforço dos cosmonautas a estação foi salva, mas o objetivo desse blog não é falar sobre isso, e sim sobre algo que ocorreu depois [1,2].
Em certo momento, na estação, Vladimir desparafusou uma porca borboleta de uma barra rosqueada, e ao sair desta, a porca manteve um movimento de translação e de rotação. Até aí tudo bem, no ambiente de imponderabilidade da estação isso era esperado. Mas na sequência ocorreu algo bem peculiar e contra intuitivo: o eixo em torno do qual a porca estava rotacionando girou 180° (para o lado oposto), depois de um certo tempo girou 180° para a posição original e continuou nesse ciclo. Não havia motivo razoável do porquê disso [2,3].
A explicação desse efeito envolve alguns conceitos físicos que podem não ser muito familiares, por isso recomenda-se ver a referência [2], que ilustra de forma visual o fenômeno.
Tal explicação vem de resultados da Mecânica Clássica, que eram, todavia, pouco conhecidos na época, já que a maioria dos autores renomados não mencionam esse fenômeno [2]. Acontece que a porca é um corpo rígido assimétrico, ou seja, os momentos principais de inércia da rotação em torno dos três eixos principais de inércia são todos diferentes [4].
Para ficar claro, o momento de inércia de um corpo é a dificuldade para colocá-lo em rotação (assim como a massa de um corpo representa o grau de dificuldade para colocá-lo em movimento de translação), e está relacionado a sua distribuição de massa. Os eixos principais de inércia de um corpo são definidos conforme a sua simetria, e os momentos de inércia das rotações em torno desses eixos são os momentos principais de inércia [4,5].
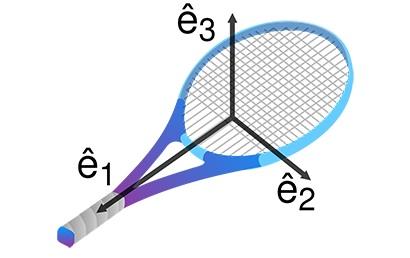
Uma raquete de tênis apresenta essas características. Observando a imagem deste blog temos o seguinte: ê1, ê2 e ê3 são os vetores unitários ao longo da direção dos eixos principais; o momento de inércia da rotação em torno do eixo ê1 é I1, de ê2, I2, e de ê3, I3. Eles obedecem a seguinte relação: I1 é maior que I2 que é maior que I3 (I1 > I2 > I3). Se a raquete for colocada para girar em torno do eixo ê2, que tem o momento de inércia intermediário, acontecerá o efeito Dzhanibekov, mas não acontecerá se girar em torno de ê1 ou ê3 [2]. De acordo com a Mecânica Clássica, o primeiro caso é instável, e o segundo, estável [4,6].
Esse efeito também é chamado de Teorema da Raquete de Tênis ou Teorema do Eixo Intermediário. Outros objetos com essas características, como um livro ou um smartphone, também apresentam esse efeito [2].
Outros fatores, como a força centrípeta, tensões no corpo e leis de conservação, também entram em cena. Os detalhes fogem do escopo deste blog, e podem ser vistos na referência [6], com a explicação dada por Terence Tao, um dos maiores matemáticos atuais [2,6].
O efeito Dzhanibekov permaneceu obscuro por muitos anos, já que, apesar de ter explicação teórica, nunca tinha sido observado no espaço. A descoberta de Dzhanibekov permaneceu em segredo durante 10 anos na União Soviética, pois pensava-se que a Terra, sendo um corpo em rotação no espaço, também teria seu eixo de rotação invertido (e que talvez estivesse relacionado com a inversão dos polos magnéticos). Inclusive isso ganhou popularidade em 2012, quando o fim do mundo era esperado com o fim do calendário maia [2,3].
Felizmente, isso se prova incorreto. A Terra, assim como todos os corpos celestes (planetas, asteroides), têm eixos de rotação extremamente estáveis [2].
Autor: Cristhian Gean Batista Guimarães.
Referências:
Referência da imagem: https://en.wikipedia.org/wiki/Tennis_racket_theorem#/media/File:Tennis_racquet_principal_axes.svg.
[1] MIRANDA, Felipe. O bravo resgate da estação espacial soviética Salyut 7. SoCientífica, 2020. Disponível em: https://socientifica.com.br/o-bravo-resgate-da-estacao-espacial-sovietica-salyut-7/.
[2] Veritasium. The Bizarre Behavior of Rotating Bodies. YouTube, 19 de outubro de 2019. Disponível em: https://youtu.be/1VPfZ_XzisU. Acesso em: 12 de fev. de 2023.
[3] PETROV, A. G., VOLODIN, S. E. Janibekov’s Effect and the Laws of Mechanics. Doklady Physics, v. 58, n. 8, p. 349–353, 2013.
[4] LANDAU, L., LIFCHITZ, E. Mecânica. São Paulo: HEMUS, 19–.
[5] LEMOS, N. Mecânica Analítica. São Paulo: Livraria da Física, 2013.
[6] Terry Tao (https://mathoverflow.net/users/766/terry-tao), The “Dzhanibekov effect” – an exercise in mechanics or fiction? Explain mathematically a video from a space station. Disponível em: https://mathoverflow.net/q/82020. Acesso em: 12 de fev. de 2023.